Die Stichprobengröße bei Umfragen verstehen
Du musst nicht jeden befragen, um verlässliche Ergebnisse zu erhalten. Eine richtig dimensionierte Stichprobe kann eine viel größere Grundgesamtheit mit bekannter Genauigkeit repräsentieren.
Dieser Leitfaden erklärt, wie die Stichprobengröße funktioniert, warum sie wichtig ist und wie du häufige Fehler vermeidest. Nutze den Stichprobengrößen-Rechner, um deine erforderliche Stichprobengröße zu berechnen.
Warum die Stichprobengröße wichtig ist
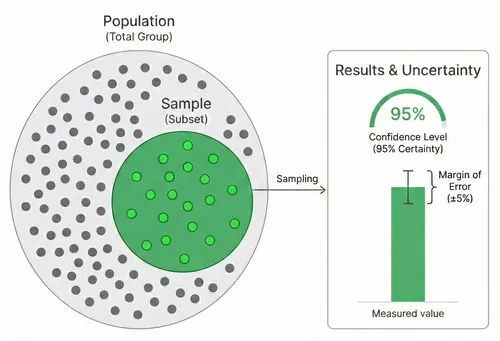
Die Stichprobengröße beeinflusst zwei Schlüsselfaktoren:
- Fehlermarge: Wie nah deine Stichprobenergebnisse am wahren Wert der Grundgesamtheit liegen.
- Konfidenzniveau: Wie sicher du sein kannst, dass deine Ergebnisse innerhalb der Fehlermarge liegen.
Wenn du die Stichprobengröße falsch wählst, verschwendest du entweder Ressourcen, indem du zu viele Personen befragst, oder du erhältst unzuverlässige Ergebnisse von zu wenigen.
Schlüsselkonzepte
Größe der Grundgesamtheit
Die Gesamtzahl der Personen, die an deiner Umfrage teilnehmen könnten. Dies könnten sein:
- Alle deine Kunden (z. B. 50.000)
- Mitarbeiter in deinem Unternehmen (z. B. 500)
- Nutzer einer bestimmten Funktion (z. B. 10.000)
- Besucher deiner Website im letzten Monat (z. B. 100.000)
Bei sehr großen Grundgesamtheiten (100.000+) ändert sich die Stichprobengröße kaum, da du bereits eine statistische Signifikanz erreichst.
Konfidenzniveau
Wie sicher du sein möchtest, dass deine Stichprobenergebnisse die wahre Grundgesamtheit widerspiegeln.
| Konfidenzniveau | Interpretation |
|---|---|
| 90 % | Du bist zu 90 % sicher, dass der wahre Wert innerhalb deiner Fehlermarge liegt. |
| 95 % | Branchenstandard - 95 % Sicherheit |
| 99 % | Sehr hohe Sicherheit, erfordert eine größere Stichprobe |
Verwende 95 %, es sei denn, du hast einen bestimmten Grund, dies zu ändern. Dies ist der Standard für Geschäftsentscheidungen.
Fehlermarge
Der akzeptable Fehlerbereich in deinen Ergebnissen. Wenn deine Umfrage eine Zufriedenheit von 60 % mit einer Fehlermarge von ±5 % ergibt, liegt der wahre Wert zwischen 55 % und 65 %.
| Fehlermarge | Anwendungsfall |
|---|---|
| ±3 % | Entscheidungen mit hohem Einsatz, die Präzision erfordern |
| ±5 % | Standard für die meisten Unternehmensumfragen |
| ±10 % | Explorative Forschung oder Umfragen mit begrenzten Ressourcen |
Kleinere Fehlermargen erfordern größere Stichproben. Eine Fehlermarge von ±3 % benötigt etwa 2,5-mal mehr Antworten als eine von ±5 %.
Die Formel zur Berechnung der Stichprobengröße
Dieser Leitfaden verwendet die Cochran-Formel, angepasst für endliche Grundgesamtheiten.
Schritt 1: Berechnung der anfänglichen Stichprobengröße (unendliche Grundgesamtheit)
n₀ = (Z² × p × (1-p)) / e²Wobei:
- Z = Z-Wert für dein Konfidenzniveau (1,96 bei 95 %)
- p = Erwarteter Anteil (0,5 für maximale Variabilität)
- e = Fehlermarge als Dezimalzahl (0,05 für 5 %)
Schritt 2: Anpassung für eine endliche Grundgesamtheit
n = n₀ / (1 + (n₀ - 1) / N)Wobei:
- N = Größe deiner Grundgesamtheit
- n₀ = Anfängliche Stichprobengröße aus Schritt 1
Du musst das nicht manuell lösen - das erledigt der Rechner.
Warum wir p = 0,5 verwenden
Der Anteil (p) repräsentiert die erwartete Verteilung der Antworten. Wenn du eine Ja/Nein-Frage stellst, bedeutet p = 0,5, dass du eine 50/50-Aufteilung erwartest.
Wir verwenden 0,5, weil:
- Es die größte (konservativste) Stichprobengröße ergibt
- Du nicht vorhersagen musst, welche Ergebnisse du erhalten wirst
- Es die sicherste Annahme ist, wenn du keine Vordaten hast
Wenn du weißt, dass dein Anteil extrem ist (z. B. 90 % Ja), kannst du eine kleinere Stichprobe verwenden - aber nur, wenn du über solide Vordaten verfügst.
Rücklaufquoten & Einladungen
Deine erforderliche Stichprobengröße ist nicht die Anzahl der Personen, die du einlädst. Du musst die Rücklaufquoten berücksichtigen.
Typische Rücklaufquoten bei Umfragen
| Umfragetyp | Rücklaufquote |
|---|---|
| In-App/Eingebettet | 20-40 % |
| E-Mail (Kunden) | 10-30 % |
| E-Mail (Mitarbeiter) | 30-50 % |
| Nach einer Transaktion | 15-25 % |
| NPS-Beziehungsumfragen | 10-20 % |
Formel: Anzahl der einzuladenden Personen = Stichprobengröße ÷ Erwartete Rücklaufquote
Wenn du 400 Antworten brauchst und eine Rücklaufquote von 20 % erwartest:
- 400 ÷ 0,20 = 2.000 einzuladende Personen
Häufige Fehler
Ignorieren der Rücklaufquoten
Zu berechnen, dass du 400 Antworten brauchst, aber nur 400 Personen einlädst, garantiert unzureichende Daten.
Verwendung der Populationsgröße als Stichprobengröße
„Wir haben 10.000 Kunden, also benötigen wir 10.000 Antworten.“ Das stimmt nicht. Etwa 370 Antworten geben dir eine Genauigkeit von ±5 %.
Vergessen von Untergruppen
Wenn du planst, nach Segmenten (Region, Produkt, Kundentyp) zu analysieren, benötigt jede Untergruppe eine angemessene Stichprobengröße. Möglicherweise brauchst du 400 Antworten pro Segment, nicht 400 insgesamt.
Nichtberücksichtigung des Non-Response-Bias
Wenn nur zufriedene Kunden antworten, repräsentieren deine Ergebnisse nicht alle. Strebe Rücklaufquoten von über 20 % an, um Verzerrungen zu minimieren.
Übermäßige Präzision
Eine Fehlermarge von ±3 % klingt besser als ±5 %, erfordert aber 2,5-mal mehr Antworten. Für die meisten Geschäftsentscheidungen ist ±5 % ausreichend.
Wann die Regeln zur Stichprobengröße nicht gelten
Standardberechnungen der Stichprobengröße gehen von Folgendem aus:
- Zufallsauswahl: Jeder hat die gleiche Chance, ausgewählt zu werden
- Repräsentative Antworten: Die Antwortenden sind den Nicht-Antwortenden ähnlich
- Einzelne Grundgesamtheit: Du misst eine Gruppe und vergleichst keine Gruppen
Diese Annahmen treffen nicht zu, wenn:
- Du selbst ausgewählte Freiwillige befragst
- Die Rücklaufquoten sehr niedrig sind (unter 10 %)
- Du eine Längsschnittstudie durchführst
- Du es mit sehr spezifischen Nischenpopulationen zu tun hast
In diesen Fällen hängt die statistische Genauigkeit mehr von der Stichprobenmethode als von der Stichprobengröße ab.
Best Practices
Definiere deine Grundgesamtheit klar
Wen genau befragst du? „Unsere Kunden“ ist vage. „Aktive Kunden, die in den letzten 12 Monaten einen Kauf getätigt haben“ ist spezifisch.
Verwende geschichtete Stichproben für heterogene Grundgesamtheiten
Wenn deine Grundgesamtheit aus unterschiedlichen Segmenten besteht, ziehe aus jedem Segment eine proportionale Stichprobe, um die Repräsentativität zu gewährleisten.
Plane die Analyse im Voraus
Wenn du die Ergebnisse nach Regionen aufschlüsselst, stelle sicher, dass jede Region genügend Antworten hat. Drei Antworten aus Asien sind statistisch nicht aussagekräftig.
Dokumentiere deine Methodik
Notiere die Größe deiner Grundgesamtheit, die Stichprobenmethode, die Rücklaufquote und die Fehlermarge. Dies verleiht deinen Ergebnissen Glaubwürdigkeit.
Berücksichtige die anstehende Entscheidung
Eine Fehlermarge von ±10 % mag für explorative Forschung in Ordnung sein. Für Entscheidungen, die Millionen von Dollar betreffen, solltest du in eine Präzision von ±3 % investieren.
Häufig gestellte Fragen
Was ist, wenn ich die genaue Größe meiner Grundgesamtheit nicht kenne?
Schätze konservativ. Wenn du denkst, dass du 5.000-10.000 Kunden hast, verwende 5.000. Bei sehr großen Grundgesamtheiten (50.000+) ist die genaue Zahl kaum von Bedeutung.
Ist größer immer besser?
Nicht unbedingt. Über die Mindeststichprobengröße hinaus haben zusätzliche Antworten einen abnehmenden Ertrag. Der Sprung von 400 auf 4.000 Antworten ändert die Fehlermarge von ±5 % auf ±1,5 % - was den Aufwand selten wert ist.
Was ist mit qualitativem Feedback?
Berechnungen der Stichprobengröße gelten für quantitative Daten (Zahlen, Prozentsätze). Bei offenen Fragen erreichst du oft eine „Sättigung“ (es tauchen keine neuen Themen mehr auf) mit 20-30 durchdachten Antworten.
Wie kann ich die Rücklaufquoten erhöhen?
- Halte Umfragen kurz (maximal 5 Minuten)
- Versende zu optimalen Zeiten (Dienstag-Donnerstag, 10-14 Uhr)
- Verwende Personalisierung in den Einladungen
- Erkläre, warum das Feedback wichtig ist
- Biete gegebenenfalls Anreize
Nächste Schritte
Nutze den Stichprobengrößen-Rechner, um dein Ziel zu bestimmen, und sieh dir dann unsere Umfragevorlagen an, um loszulegen.